
The Official Lotto Odds Are Correct as Exactly, Not At Least ~
Calculated by Hypergeometric Distribution Probability Formula
By Ion Saliu, ★ Founder of Lotto Mathematics



Axiomatic ones, I was thinking that the official lotto odds were wrong. I held an extremely strong opinion up until this moment, November 15, 2001.
• My strong opinion was determined by the game of roulette and the fundamental formula of probability: p = n / N. There are 38 numbers in the double-zero roulette. There is a straight-up bet: Betting on a single number to hit. The probability to win a straight-up bet is 1 in 38. If I play two distinct numbers, my winning chance (still probability) is 2/38. I haven't heard anybody contest this.
Based on that, I extended it to lotto. I applied the same formula: p=n/N. For a lotto 6/49 game, n=6, N=49, therefore the probability to get one number out of 6 is p=6/49. I am correct only insofar as I ONLY SELECT ONE NUMBER. That is, I only play one number, like at roulette. In that case, my winning chance is 6 in 49. Problem is, I MUST play 6 lotto numbers! That's the rule. In such a case, the probability is totally different. Also, the probability to get 2 out of 6, following my now-abandoned method, was different from the official probability (official lottery commission odds). Again, my method was applied to playing a ticket with two numbers only, which is not accepted in any lottery!
•• The official lotto odds are calculated by the so-called hypergeometric distribution probability formula. I had a serious problem with that probability because it divides the elements (lotto balls) in two divergent categories. The winning numbers are in one group; the opposite elements are in the other group. Then numbers are drawn randomly, including from both groups. It looks like a contradiction in terms: drawing BOTH winning and NON-winning numbers! Then I realized I could overcome the contradiction by considering the balls drawn as the winning numbers; the remaining balls were the “losing” numbers! It made sense. In such case, applying the hypergeometric distribution is the correct method of calculating the lotto odds. And since the player must select (play) 6 numbers, particular cases must be excluded. For example, a case such as 1 of 6 in a lotto 6/10 game is NOT possible.
••• I had also a strong connection with the theory of lotto wheels. Without a doubt, the official lotto odds do NOT offer the same guarantee as a lotto wheel. For example, the odds to get 3 of 6 in a lotto 6/49 game are 1 in 56. Nobody will ever be able to construct such a tight wheel. The distinction between the odds and the wheels is significant. The wheels offer a minimum guarantee (e.g. 3 out of 6). There are situations when the wheels offer more than just 3 of 6 or any other minimum guarantee. The odds refer to EXACTLY 3 of 6.
But if the odds are correct, they should be validated by the NUMBER OF WINNERS in a draw. The number of winners of a specific prize (game) is direct proportionate with the probability of winning the prize. Or: The harder the game, the fewer the winners. I verified online for Pennsylvania lottery game 5/39. The odds of winning 5 of 5 are 1 in 575,757. The odds of winning 4 of 5 are 1 in 3,386, or 575,757 / 3,386 = 170 times better than the 5 of 5 case. Guess what? The number of 4 of 5 winners averages out to around 170 for every 5 of 5 winner!
•••• Axiomatic ones, my probability software OddsCalc calculates the odds of any lotto game, including Powerball, Mega Millions, Euromillions, Keno. If the game draws 6 winning numbers, the program calculates the odds from 0 of 6 to 6 of 6. Of course, 6 of 6 represents the lotto jackpot case.
OddsCalc calculates the lotto odds using the hypergeometric distribution probability. The odds are calculated as exactly k of m in n from N.
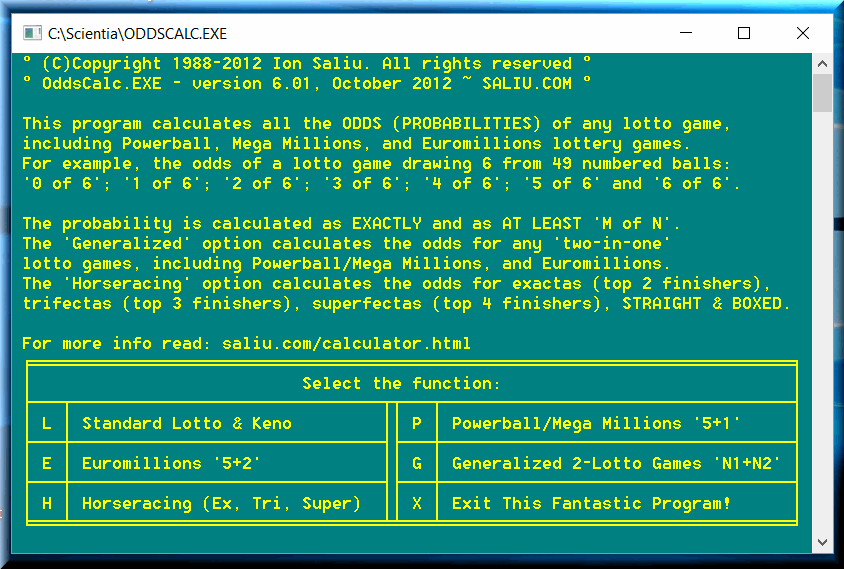
See also the resource Random Generator, Odds Calculator in the footer of most Web pages at SALIU.COM.
Well, one should listen to some dreams, sometimes. I was in Atlantic City. I only saw two casinos. I was surprised. I asked: “Where are the other casinos?” A pretty lady dealer answered: “They are all here, eight of them.” Yet, I could see only two buildings. “It's eight. Look towards the ocean!” That dream made me think. I put aside my work at the new version of MDIEditor and Lotto. I took a deck of cards (casinos, right?) I chose my favorite number: 9. I dealt 6 cards at a time (“lotto draw”). Since the probability was 6/10 (60%), the results followed the probability very closely. Then I shouted to myself: “You are playing a form of roulette, not lotto!” And that is how I created that piece of great probability software calculator, OddsCalc!
The odds calculated as EXACTLY in a lotto game 6/49:
0 of 6 in 6 from 49: 1 in 2.29
1 of 6 in 6 from 49: 1 in 2.42
2 of 6 in 6 from 49: 1 in 7.55
3 of 6 in 6 from 49: 1 in 56.66
4 of 6 in 6 from 49: 1 in 1032.4
5 of 6 in 6 from 49: 1 in 54200.84
6 of 6 in 6 from 49: 1 in 13983816
The odds calculated as AT LEAST in a lotto game 6/49:
0 of 6 in 6 from 49: 1 in 1
1 of 6 in 6 from 49: 1 in 1.77
2 of 6 in 6 from 49: 1 in 6.62
3 of 6 in 6 from 49: 1 in 53.66
4 of 6 in 6 from 49: 1 in 1013.03
5 of 6 in 6 from 49: 1 in 53991.57
6 of 6 in 6 from 49: 1 in 13983816



